One
First, we have to distinguish:
What is the difference between investment, speculation, and gambling?
It seems that these three are full of uncertainty.
Entrepreneurs and investors often like to say: Let's take a gamble.
Speaking of it, it seems that they are all betting on the invisible future:
Winning the bet is the investment success;
Win thrills and earn a lot is speculation success;
Failure is considered "lost the gambling".
Who is not to bet on one life?
This kind of thinking is in fact a self-defeating and abandoning without making progress and thinking.
In order to avoid falling into meaningless logic and word games, here, I want to use a simple and crude way to define:
The expected value is positive, it is investment;
The expected value is negative, it is gambling;
The unknown is speculation.
A guest official with investment experience may say, are you nonsense? Since we are talking about uncertainty, it is difficult to tell whether the expected value is negative. If you know the expectations, who won't make money?
Is it true?
not necessarily.
The first few parts of this article seem simple. However, in reality, most of the mistakes we make appear in simple common sense.
I integrated the uncertainty of the event, the uncertainty of time and the uncertainty of the bargaining chip together, to explore how to use probability thinking to build a system.
Why not relive it together?
two
Although the concept of expected value is very simple, there are not many people who can really understand it, perhaps less than 1% of the crowd.
I once turned over a best-selling book that was said to have sold hundreds of thousands of copies. There was a section on probability. The author actually confused basic concepts such as probability, odds, and expected value.
Let's review the expectations from the beginning:
In probability theory and statistics, the expected value of a discrete random variable (or mathematical expectation, also referred to as expectation, or expected value in physics) is the sum of each possible outcome in an experiment multiplied by its outcome probability.
In other words, the expected value is like a random experiment repeated many times under the same opportunity, and the average result of all the possible states is basically equivalent to the expected number of the "expected value".
For example, if you keep throwing a dice many, many times, the probability of you getting each one is the same, then your expected value of throwing a dice is:
Then, it can be calculated that for a fair six-sided die, the expected value of each "point" is 3.5.
This is an average value obtained after an infinite number of repetitions.
three
Such a simple framework is the first formula that almost all investment professionals must have.
Rubin cited a case of Goldman Sachs' investment arbitrage.
Once, after two companies announced a merger, Goldman Sachs planned to do an arbitrage.
Despite the announcement, the merger may succeed or fail.
Goldman Sachs intends to buy W company, the stock price was 30.5 US dollars.
If the merger is negotiated, the share price of W company may rise by $3;
If the merger fails, company W’s stock price may fall by about $6.
This is equivalent to an estimate of the numbers on the dice, and then we have to estimate the possibility of each side.
The probability of success of the merger is set at approximately 85%, and the probability of failure is 15%.
Next, let's calculate the expected value: the possible increase in the stock price is $3 times 85%, and the risk of a fall is $6 times 15%.
US$3×85%=(May increase) US$2.55
-6 USD × 15% = (may fall) -0.9 USD
Adding the two together, the expected value of the investment is $1.65 per share.
The investment plan will be completed within three months:
The expected value per share is $1.65
The principal is $30.50
The possible return in 3 months is 5.5%,
The annualized rate of return may be 22%.
Ordinary people may feel confused when looking at this case:
How much money will rise or fall is guessed, and the possibility of rise or fall is also guessed. Does this calculation make sense?
The calculation of expected value provides an analysis framework for decision-making and betting in the uncertain future.
The possible rise and fall of the stock price depends on professional ability and experience.
Whether the transaction can be completed depends on professionalism and intelligence.
No matter how high the level of the above two things is, they also need to be placed under the analysis framework of expected value calculation to dance with uncertainty.
No matter how accurate this transaction is predicted, the result may be unexpected and far from the expected value.
It's like throwing a dice, the expected value is 3.5, but the probability of you throwing a 6 is still 1/6.
However, if you throw it many times, you will be very close to the expected value.
Therefore, the calculation of the expected value provides a kind of "fuzzy accuracy". The more repetitions, the more accurate.
four
Although the calculation is so simple, many professionals are confused by the expected value.
Taleb once ridiculed Soros' former partner Rogers, saying that he made too much money for a guy like him who didn't even understand his expectations.
It seems that many people on Wall Street don't understand. Taleb said at an investment seminar: "I believe the probability of a slight increase in the market next week is very high, about 70%." However, he shorted the S&P 500 index futures a lot, betting that the market would fall.
Many people didn't understand what it meant. His opinion is: the possibility of the market rising is relatively high (I am optimistic about the market outlook), but it is best to sell short (I am optimistic about the outcome), because in case the market falls, it may fall by a large margin.
Suppose next week the market has a 70% probability of rising and a 30% probability of falling. But if the rise will only rise by 1%, the fall may fall by 10%. The expected result in the future is: 70%×1%+30%×(-10%)=-2.3%, so it should bet on the decline, and the chance of short selling stocks is greater.
Let us return to the point at the beginning of this article:
The expected value is positive, it is investment;
The expected value is negative, it is gambling;
The unknown is speculation.
The case of Goldman Sachs seems to be an investment with positive expectations.
Taleb's bet looks like speculation with unknown expectations (just "I believe").
What about gambling?
Take American roulette as an example:
There are 38 numbers on the commonly used roulette, and the probability of each number being selected is equal, which is 1/38.
You bet on a certain number. If you bet, you earn 35 times the bet (the bet is not included). If you don't bet, you lose the bet.
Let's calculate the expected value. If you bet 1 yuan each time:
The probability of winning is 1 in 38, and you can get 35 yuan;
The probability of losing is 37/38, losing 1 yuan.
35×1/38-1×37/38, the result is approximately equal to -0.0526 yuan.
Maybe you will accidentally bet, the cost has become 36 times, or even bet several times, but as long as you keep playing, the law of large numbers will come into play and you will lose all your capital steadily.
Therefore, in this world, perhaps only the owner of the casino makes money by the probability of "stable".
Conversely, if you are a gambler who wants to pursue a stable probability, you will lose very stably and poorly very stably.
More than gamblers, in reality, people are willing to do anything for the sake of illusory certainty.
Fives
Well, suppose we all know the concept of "expected value", and temporarily assume that we are very reliable in estimating the increase and decrease and the corresponding probability of occurrence, then can we go on the road to becoming an investment master?
Or not.
In 2016, physicist Ollie Peters and Nobel Laureate in Physics Murray Gellman wrote a paper on ergodicity with an example:
There is a coin gambling game, you put in 1 yuan, 50% can get 0.6 yuan, 50% can get 1.5 yuan.
Calculated according to the expected value, half the probability of loss is 40%, and half of the probability is profitable 50%. The mathematical expectation is 5%.
In popular words, this is a high probability of making money. You can play this game boldly.
However, there are two ways to play this game. To be precise, there are two different ways of betting:
Method a: You play with 1 yuan every time. Assuming you have an unlimited number of 1 yuan, you can keep playing . In the long run, you will definitely make money. On average, 5% of the mathematical expectation for each game is considered to be 0.05 yuan.
The disadvantage is that it is too slow, and you must have enough time to play.
Method b: Take out the largest amount of money you can spend and invest in it.
The latter method of play is called All in. It seems extreme. In fact, many people do this. I have experienced it myself. Who has never been young (stupid).
Let's make a simple calculation.
Your principal is one million, the first one wins, the second one loses, and the third one wins, and so on.
Intuitively, with 1 million principal, if you win, you will earn 500,000, and if you lose, you will lose 400,000. Why can't you play?
Take a piece of paper and use the mathematics ability of the current kindergarten class in China to calculate:
1 million ✖️(1+50%)✖️(1-40%)✖️(1+50%)(1-40%)......
If you keep playing like this, you will find that there will be no money after a few.
Isn't this the reality that most ordinary people make investments?
The leek is more painless after being cut. Maybe you still feel that you didn't pose when you were cut, and continue to study and practice every day, and then take the hard-earned money to the next outlet of All in.
The key to the calculation here is the difference between the arithmetic mean and the geometric mean.
Suppose you bought a fund for 1 million, and it rose by 100% in the first year and fell by 50% in the second year. So what is your profit?
According to the arithmetic mean:
Average return rate = (first year return rate + second year return rate)/2=(100%-50%)/2 = 25%.
Calculated according to the geometric mean:
The annual return rate is assumed to be x, (1+x)×(1+x)=(1+100%)×(1-50%)=1, the calculation result, x=0.
In other words, according to the geometric mean, the annual rate of return is zero. This is actually the case.
The rate of return calculated here with the geometric mean is the so-called "annualized rate of return".
In contrast:
"Annualized rate of return" (geometric average rate of return) more accurately reflects the actual historical return of the fund;
The arithmetic average rate of return magnifies the rate of return on investment.
Next time you buy a fund, remember to ask:
How long is this fund? Is this rate of return an arithmetic average or a geometric average?
six
So far, another element related to "uncertainty" has appeared, that is:
Bargaining chips.
The expected value provides a framework for the uncertainty of events and time, but does not include chips.
Even if you have enough insight into uncertain events, if you can't grasp the number of bets, time will not be your friend in overcoming uncertainty.
If your bet ratio is too small, you may earn too slowly;
Your bet ratio is too large, you may lose your principal;
Even if the probability of winning is greater, the expected value is positive. If you all in again and again, you may be cut out of the leeks because of the geometric mean.
At this time, an investment truth emerged:
You must survive before you succeed.
The financial legend Thorpe found in his attempt to defeat the casino that even if you have insight into the casino’s loopholes and found opportunities with positive expectations, you have to face the challenge of “how to determine the size of the bet”.
Shannon, another genius, suggested that he refer to an article published by John Kelly in 1956.
Shannon modified it slightly and used it as a betting principle for blackjack, roulette, other gambling, sports betting, and the stock market.
The Kelly formula follows the principle of maximizing the geometric mean. Using this formula to determine the proportion of each bet amount to the principal can allow investors to maximize the geometric mean of the portfolio's return in each period.
Economists have long disputes about the geometric mean and Kelly's formula, but for ordinary people, there is only one thing to remember:
No matter how powerful the Kelly formula is, it is only valid for bets with "positive expectations".
Simply put, this formula only helps people who want to make valuable investments, and it is meaningless for gambling (negative expectations).
This is why I use expected value to distinguish investment, speculation and gambling.
Seven
Let us look back at Kelly's formula.
What the formula does not emphasize is:
Is your principal fixed?
In other words, will the principal you use to bet more and more like spring water?
One of the biggest differences between professional investors and amateur investors is that professional players have a steady stream of ammunition.
Buffett has a float from an insurance company that can issue bonds (he borrowed US$1.8 billion from Japan in April this year).
He also emphasized that the company he invested in has a good free cash flow. He has a very small headquarters and only cares that the managers of the companies under his company continue to hand in the money they make.
According to people familiar with the matter, Hillhouse is raising as much as US$13 billion from investors in the first half of 2020, preparing to seize new opportunities in the economy under the epidemic.
The last financing was in 2018, and finally raised $10.6 billion, a record.
According to data from the University of Texas Endowment Fund, after deducting expenses, Hillhouse's average annual return for the past ten years as of June 2019 is about 20%.
Some people may be surprised that such a great company has a "only" 20% annual return!
Of course, the fact is that the return of 20% per year for ten consecutive years is already amazing.
The point is that even bulls such as Buffett and Hillhouse are constantly getting funds to prepare chips for the next bet.
Only in this way, the infinite game can continue, the hero stays on the field all the time, the law of large numbers plays a role, and wealth is worth realizing because of the probability advantage in ergodicity and the maximization of positive expectations.
This is the truth behind "long-termism".
Eight
It is difficult to invest, to bet on the future, to make money from uncertainty, it is difficult for everyone.
No one makes money by crystal ball.
When Weilai was listed in 2018, Hillhouse's shareholding in Weilai was as high as 7.5%.
In 2019, Zhang Lei continued to bet on the new energy vehicle track, increasing his holdings of Weilai to 12%, and also bought 668,300 new Tesla shares.
As a result, because of the decline in subsidies for new energy vehicles and the sale of fuel vehicles due to the introduction of the National Sixth Standard, Weilai’s stock price fell to as low as $1.
Zhang Lei then liquidated Weilai and Tesla, just before Tesla's surge.
Today, Weilai's stock price has risen back to nearly $28.
To cite the examples of Weilai and Tesla, it is not that Zhang Lei is not good, nor is it imagining that some articles talk about "Zhang Lei's long-termism you can't learn", but want to say:
1. No one can predict the short-term future. It is normal to "wrongly see" a certain investment at a certain time;
2. A mature investor does not need to maintain his "extremely correct", he only needs to win from the level of probability and expectation;
3. As an increasingly large fund, the investment in certain areas will be closed as soon as possible, avoiding drawdowns, and achieving a better geometric average return;
4. Hillhouse turned his head back in July 2020 and made a lot of money for Xiaopeng Motors.
nine
Maybe you still remember a fire that I planted at the beginning:
On what basis do you estimate the expected value of an investment?
How do you know that if you buy a stock, it may rise by 10 yuan, and the probability of occurrence is 60%; it may fall by 5 yuan, and the probability of occurrence is 40%.
With so many possibilities added together, isn't it even more impossible?
Expected value calculation provides a framework to deal with uncertainty;
The Kelly formula provides a criterion for betting based on the principal ratio;
Obtaining funds provides investors with a steady stream of ammunition.
However, to achieve 20% annual returns like Hillhouse, you need to do more.
In a nutshell:
One is to obtain better investment targets:
One is to intervene in the company to increase the probability of value increase, so as to actively increase the expected value of project returns.
The former, I call it resources;
Or, it is empowerment.
Zhang Lei uses his alumni circle in the National People's Congress and Yale to the fullest. He will host the elites of the investment circle and the business circle on luxury yachts in Hong Kong. The connections in the Eastern countries are more important for investment.
As for empowerment, there are more cases in this area, through cooperation and technology.
Because of resources, better projects can be obtained;
Because of empowerment, the expected return value of the project can be higher.
After completing the above, coupled with timing and luck, Hillhouse has achieved 20% annual return for customers.
ten
We have never realized that we were very lucky to be born in an era full of miracles.
China’s rapid and long-term growth over the past 30 years is extremely rare in human history.
But because we are in it, we feel accustomed to it, just like people who are accustomed to high-speed trains and are accustomed to fast speed.
On the other hand, folk culture’s admiration of the top talent has actually strengthened the lottery jackpot effect, and many people think that casinos must have cheats.
People are used to gambling and worship casino winners.
People are anxious about missing real estate, about missing Tencent, and about missing Bitcoin.
There are legends of tenfold and hundredfold return everywhere, making people unable to sleep well at night.
This kind of worship of head winners, the biggest harm to ordinary people, is that people fall into the "decimal trap", mistakenly taking some extremely small probability things as normal.
However, the reality is that even in the era of rapid growth, investment is very difficult.
Few people because of low returns and poor, but too Nixdorf people because of the pursuit of higher returns and loss of light hard earned money.
Most of the money comes from the super luck of the big era, and it is almost impossible to reproduce it again.
At last
in conclusion:
1. Stay away from gambling, invest carefully, try not to speculate, and do things with positive expectations;
2. If you lose money and you make money, don’t try to make money by forecasting, rely on probability and positive expectations
3. It is difficult to invest. We must lower our expectations of obtaining excess returns and pursue reasonable returns;
4. Betting needs to control the proportion and extend the time;
5. There must be a steady stream of cash flow. Be careful of those fixed asset investments that do not generate cash flow, even if some of them may seem to have a large "rise";
6. Don't hang up before getting rich;
7. For the annual return on investment, the geometric average is more important than the arithmetic average;
8. Don't participate in those zero-sum games;
9. Work hard to create value, do value-creating work, and invest in companies that create value;
10. Regarding financial freedom, please remember: Money is like sea water. The more you drink, the thirsty you get.
Once you put finances and freedom together, you actually put on the shackles of freedom.
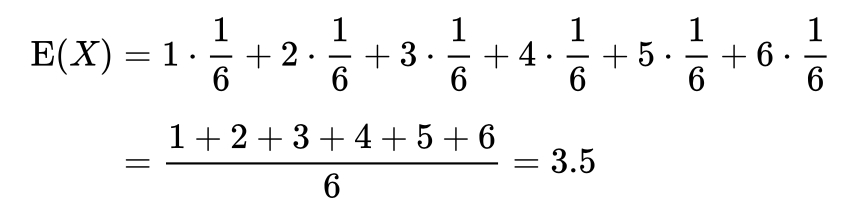
No comments:
Post a Comment